Big O Notation - 18/07/2024

Index

• Big O Notation
• Time Complexity
• Space Complexity
• Big O: O(1)
• Big O: O(n)
• Big O: O(n^2)
• Big O: Drop Non-Dominant Terms
• Big O: O(log n)
• What if we have O(n) but with two different arguments?
• Big O: Array Operations
• Better understanding

Big O Notation

Big O helps us to determine the efficiency of an algorithm. It describes the worst-case scenario for how an algorithm will perform.

Big O notation will take into account two areas: time complexity and space complexity.

Time Complexity

We don’t measure the time in seconds, but in the number of operations. If you take the same code and run it on a faster computer, the speed will be different, but the number of operations will be the same.

Space Complexity

We measure the space complexity in the amount of memory that an algorithm uses. So it also can happen that the code use less memory but more time, or vice versa. Therefore your decision on which algorithm to use will depend on the problem you are trying to solve.

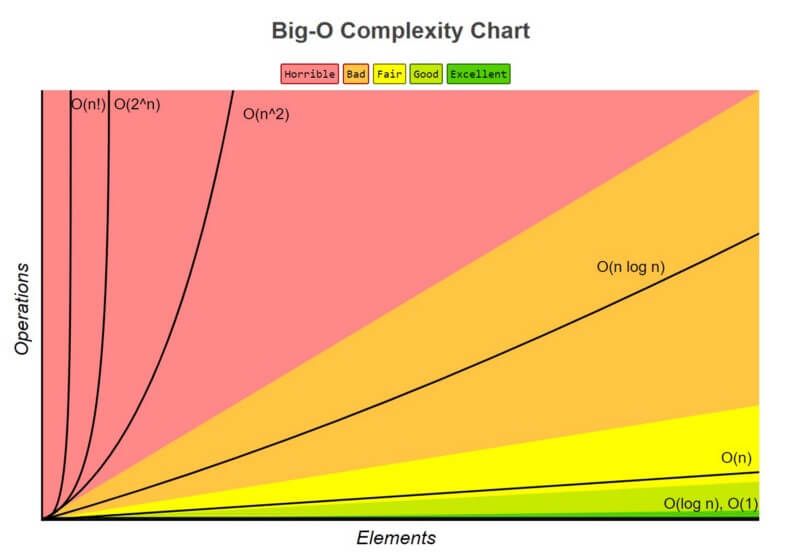
Big O: O(1) - Most Efficient 🟢

O(1) describes an algorithm that will always execute in the same time (or space) regardless of the size of the input data set.

function doSomething(n) {
  return n + n;
}

function doSomethingElse(n) {
  return n * n;
}

It doesn’t matter if n is 1 or 1,000,000, the number of operations will be one O(1).

Big O: O(n) - Medium Efficient 🟡

O(n) describes an algorithm whose performance will grow linearly and in direct proportion to the size of the input data set.

function doSomething(n){
  for (let i = 0; i < n; i++) {
    console.log(i);
  }
}

function doSomethingElse(array) {
  for (let i = 0; i < array.length; i++) {
    console.log(array[i]);
  }
  for (let j = 0; j < array.length; j++) {
    console.log(array[j]);
  }

The second function will be O(n + n) or O(2n) but we drop the constant, so it will be O(n). We drop it because it doesn’t matter if it’s 2n or 100n, it will grow linearly.

Big O: O(n^2) - Less Efficient 🔴

O(n^2) represents an algorithm whose performance is directly proportional to the square of the size of the input data set.

function doSomething(n) {
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j++) {
      console.log(i, j);
    }
  }
}

Big O: Drop Non-Dominant Terms

When you have multiple terms in a Big O notation, you drop the non-dominant terms.

function doSomething(array) {
  for (let i = 0; i < array.length; i++) {
    for (let j = 0; j < array.length; j++) {
      console.log(array[i], array[j]);
    }
  }
  for (let i = 0; i < array.length; i++) {
    console.log(array[i]);
  }
}

This will be O(n^2 + n) but:

N squared is the dominant term, because imagine that n is 100, then n^2 is 10,000 and n is 100. So the n term is not relevant.

So it will result in O(n^2).

Big O: O(log n) - More Efficient 🟢

Linear Search (O(n)): To find an element, you might have to check every element. For an array of size 8, this could take up to 8 steps.

Binary Search (O(log n)): Efficiently finds an element by repeatedly dividing the array in half.

Example

To find 1 in the array:

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8

Step 1: Compare with middle element 4, new search space: 1 | 2 | 3 | 4

Step 2: Compare with middle element 2, new search space: 1 | 2

Step 3: Find 1

For 8 elements, log2(8) = 3, so time complexity is O(log n). For 1,000,000 elements, it takes about 20 steps, making binary search much faster than linear search.

What if we have O(n) but with two different arguments?

function doSomething(a, b){
  for (let i = 0; i < a; i++) {
    console.log(i);
  }
  for (let j = 0; j < b; j++) {
    console.log(j);
  }
}

You may think that is O(n) but it’s not. It’s O(a + b) because we are not sure if a and b are the same. So we can’t drop the constant.

Big O: Array Operations

• Pushing push() to the end of an array is O(1) because you are just adding an element.
• Popping pop() from the end of an array is O(1) because you are just removing the last element.
• Shifting shift() elements from the beginning of an array is O(n) because you have to re-index all the elements.
• Unshifting unshift() elements to the beginning of an array is O(n) because you have to re-index all the elements.
• Splicing splice() is O(n) because you have to re-index all the elements.
• Concatenating concat() is O(n) because you have to copy all the elements to a new array.
• Sorting sort() is O(n log n) because it uses a comparison sort algorithm.

Better understanding

I have found this answer on Stack Overflow that I think it’s a good way to understand it:

O(1) (in the worst case): Given the page that a business’s name is on and the business name, find the phone number.

O(1) (in the average case): Given the page that a person’s name is on and their name, find the phone number.

O(log n): Given a person’s name, find the phone number by picking a random point about halfway through the part of the book you haven’t searched yet, then checking to see whether the person’s name is at that point. Then repeat the process about halfway through the part of the book where the person’s name lies. (This is a binary search for a person’s name.)

O(n): Find all people whose phone numbers contain the digit “5”.

O(n): Given a phone number, find the person or business with that number.

O(n log n): There was a mix-up at the printer’s office, and our phone book had all its pages inserted in a random order. Fix the ordering so that it’s correct by looking at the first name on each page and then putting that page in the appropriate spot in a new, empty phone book.